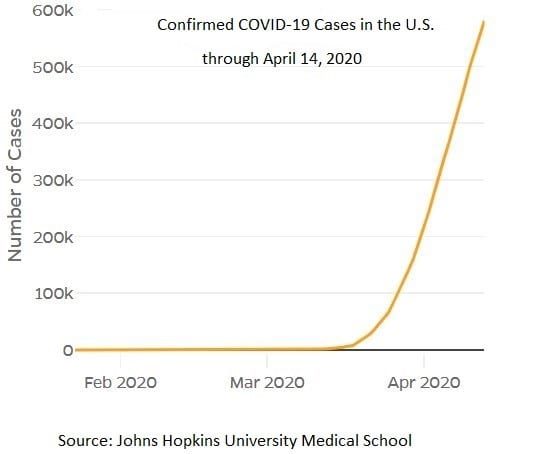
My husband and I were sitting in front of the TV, watching the grim nightly tally of confirmed coronavirus cases in the U.S. It was approaching 500,000 but just days before it had been half that. A couple of weeks ago, the number was a tenth of what it is now. It was shocking and yet, a familiar sight in mathematics. It’s the phenomenon of the exponential growth curve – something my colleagues and I have been teaching students for decades as it has pertained to population growth.

Anyone who wants to know more about how exponential growth occurs, or who is confused about what it means to “flatten the curve,” should continue reading this post.

Global Population: An Example of the Unflattened Curve

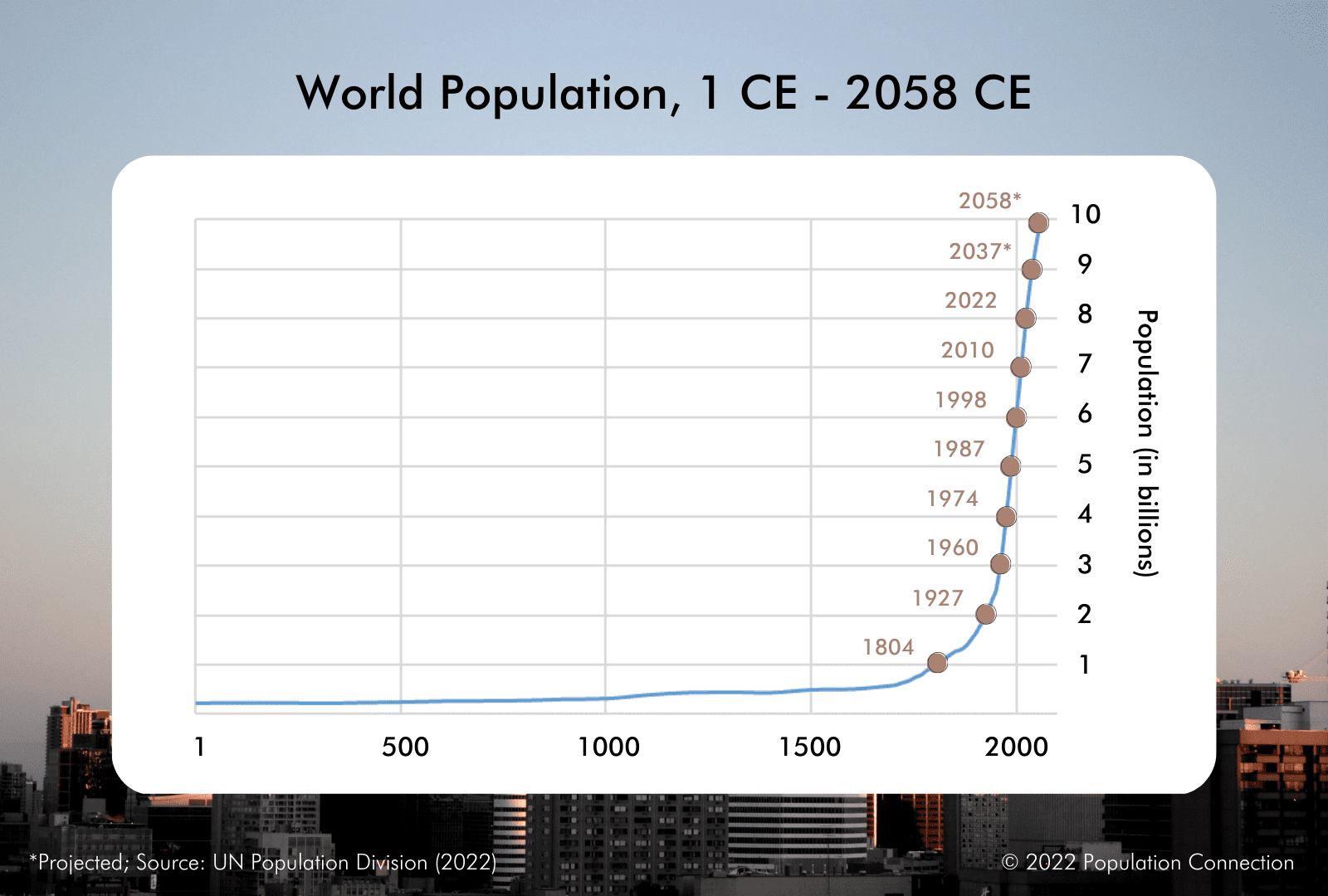
This “J-curve” as it’s often known, appears in many high school biology textbooks. When displaying human population growth, the curve begins on its upward trajectory right around the Industrial Revolution when people started to live longer, due to a variety of factors (better nutrition, sanitation, farming technology, medical knowledge, etc.). The curve then shoots straight up with the population doubling ever faster – from 1 to 2 billion in 123 years (1804-1927), then 2 to 4 billion in just 47 years (1927-1974). This growth coincides with a lot of markers of human progress, including the development of antibiotics, antiseptic practices in hospitals, and the Green Revolution.

Ideas for Teaching Exponential Growth

To help students of all ages understand this exponential growth phenomenon, we have several teaching activities that have become staples of the Pop Ed curricula. A few of them are exponential growth riddles to illustrate how starting with even a small number and continuing to double it leads to very large numbers, very quickly. In one, we ask students to imagine bacteria growing in a bottle. Starting at 11 pm, one bacterium divides into two at 11:01, two divide into four at 11:02, and so on every minute until the bottle is completely full of bacteria at midnight. At what time is the bottle “only” half full? Why, at 11:59 pm, of course! This helps students see why people often ignore signs of exponential growth until it’s very late in the going.

A great literary explanation of exponential growth for elementary students can be found in the classic picture book, One Grain of Rice. A raja (king) in India is hoarding rice while his subjects starve. A clever girl does the raja a good turn. When offered a reward of her choosing she asks for just one grain of rice, that would be doubled each day. The raja thinks her a bit daft but goes along with the scheme and laughs at her during the first week when she’s only taking home handfuls of rice. By the month’s end, though, it takes dozens of elephants to haul all of the rice from his storehouses, which the girl has him distribute to the people of the kingdom. Pop Ed has based a classroom activity on the book with worksheets for students to practice their math skills.

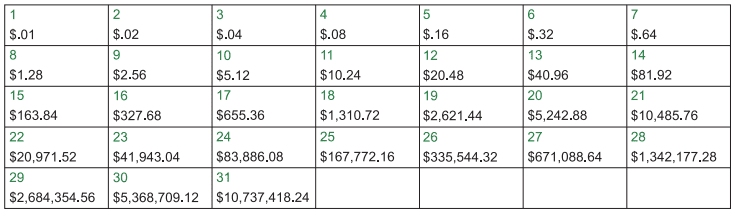
On a recent episode of NPR’s Radio Lab, a contributor remembers his father trying to teach him about exponential growth by asking which of these payment plans for mowing the lawn would be more lucrative – a one-time payment of $1 million, or a penny doubled each day of the month through the end of a 31-day month. He opted for the first choice, not realizing the second would net him over ten times as much. When he started to see the growth curves of COVID-19 cases, he remembered his father’s lesson – “this is the penny thing!”

The Flattening Curve: When Growth Slows Down

Getting back to human population growth, we are now seeing the J-curve start to flatten. Human population is still growing steadily (by over 80 million people each year!) but the global population is no longer growing ever faster. We are expected to double that 1974 population of 4 billion to 8 billion by 2023, a period of 49 years. (If we were still growing exponentially that doubling would have come in half that time.)

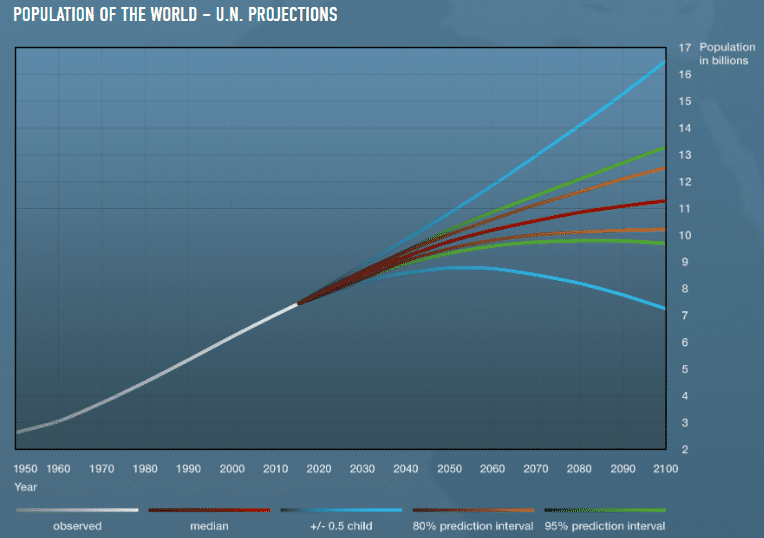
In fact, no demographer expects our population to continue doubling. Since 1974, we have added each billion people at a more linear interval of every 12-14 years (1987, 1999, 2011). At our fastest rate of growth in the mid-1960s, world population was increasing by 2.2 percent per year. The rate of growth has since halved to 1.1 percent. Demographers at the United Nations project that this rate will continue to drop until our world population growth curve flattens around the end of this century.

Both the pandemic’s spread and population growth provide examples of exponential growth. They are also models of how societies can take actions to change the trajectories of the growth, to flatten the curves. For population growth, it took intervention, coordination and social responsibility to begin to flatten the curve. This entailed concerted work to improve public and reproductive health around the globe, expand education and opportunities for girls and women, and raise the standard of living everywhere. In the case of COVID-19, we are practicing social distancing to contain the spread of the virus.

Slowing world population growth enables us to plan for the infrastructure and resources we’ll need for more people in the future, just as slowing the current pandemic will give us the time to develop vaccines, cures and shore up our healthcare infrastructure to deal with this and future medical crises.

Image credits: Graph of confirmed COVID-19 cases (Johns Hopkins University Medical School); One Grain of Rice cover (Scholastic Press)