This is the first post in a three-part series on exponential growth and doubling time – concepts that are important in not only mathematics courses, but life science and AP Environmental Science courses. The series will explore these concepts, describe the calculations involved, and provide educators with resources for teaching students about these important topics.
What is Exponential Growth?
Before we dive in to the concept of exponential growth – consider this brainteaser from our student activity Population Riddles: A father complained that his son’s allowance of $5 per week was too much. The son replied, “Okay, Dad. How about this? You give me a penny for the first day of the month, 2 cents for the second, 4 cents for the next, 8 cents for the next, and so on for every day of the month.” The father readily consented.
Who was more clever, the father or son?
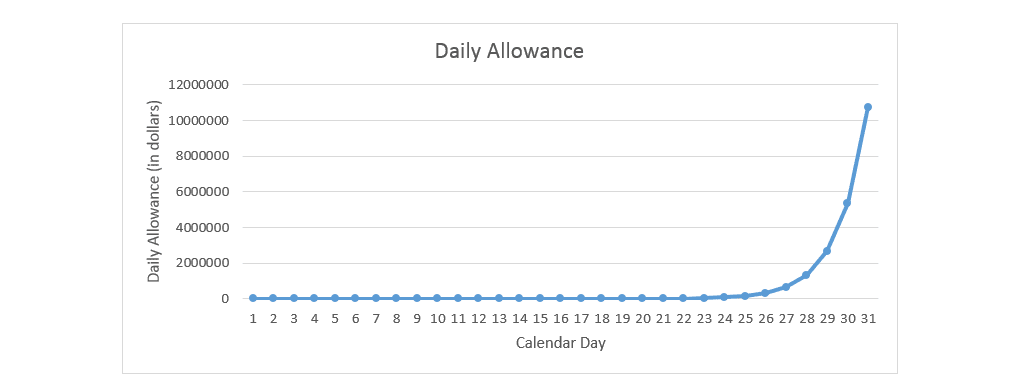
If you answered the son, you are correct! In fact, the son’s allowance on the 31st alone would total $10,737,418.24! In this riddle, students quickly learn that doubling a small number over and over soon means doubling larger numbers. This phenomenon is the driving power behind exponential growth.

Exponential growth is growth that increases by a constant proportion. In the allowance riddle, the son requested that his father double the dollar amount (or increase the amount by 100%) each day beginning at $0.01, making it a perfect example of exponential growth. It easy to identify a population experiencing exponential growth when we graph the data. Most graphs will exhibit a strong J-shape – often referred to as the “J curve”. If we look at a graph of the son’s daily allowance we can see the J curve take shape starting at day 26.
One of the best examples of exponential growth is observed in bacteria. It takes bacteria roughly an hour to reproduce through prokaryotic fission. If we placed 100 bacteria in an environment and recorded the population size each hour, we would observe exponential growth. We would record 200 at the start of the second hour, 400 at the start of the third, 800 at the start of the fourth, and so on. Eventually, we would observe a leveling off in population size due to various resource and ecosystem constraints. This is an important observation. A population cannot grow exponentially forever. Over time, it will exceed its carrying capacity – an important concept in the life and environmental sciences.
Resources for Teaching Students about Exponential Growth
Population Education has many resources for teaching students about exponential growth. Be sure to check out our website for more great lessons on exponential growth!
- Population Riddles: Riddles that help students conceptualize large number and understand the concepts of exponential growth and doubling time.
- World Population DVD: Our award winning video is a strong visual representation of human population growth over time.
Exponential Growth Series
- Post 1: What is Exponential Growth?
- Post 2: What is Doubling Time and How is it Calculated?
- Post 3: Using Popuation Growth to Explore Exponential Growth and Doubling Time



